4^ο

Κατασκευάσαμε και πετάξαμε χαρταετό διερευνώντας τις αρχές STEM που κρύβονται πίσω από αυτό, παίζοντας, δημιουργώντας και μαθαίνοντας ταυτόχρονα!

Γνωρίζατε ότι το παραδοσιακό έθιμο του πετάγματος του χαρταετού “κρύβει” γνώσεις STEM? Αν όχι ελάτε να το διερευνήσουμε μαζί!

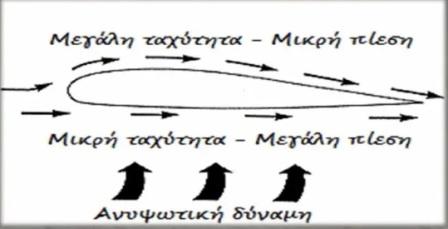
Το μυστικό για να πετάξει ψηλά ένας χαρταετός κρύβεται στα ζύγια του, τα οποία τον βοηθούν να πετάει υπό μία ορισμένη γωνία στο ρεύμα του αέρα. Για την ακρίβεια, ο αέρας που κινείται κάτω από τον χαρταετό κινείται με μεγαλύτερη ταχύτητα από τον αέρα που κινείται στο κάτω μέρος του με αποτέλεσμα να ασκείται μεγαλύτερη πίεση στο κάτω μέρος του χαρταετού από ότι στο πάνω μέρος του. Αυτό έχει σαν αποτέλεσμα να ασκείται στον χαρταετό μια συνισταμένη δύναμη που τον ανυψώνει στον ουρανό! Πίσω από αυτό το φαινόμενο κρύβεται η αρχή του Bernoulli για τη μηχανική των ρευστών.

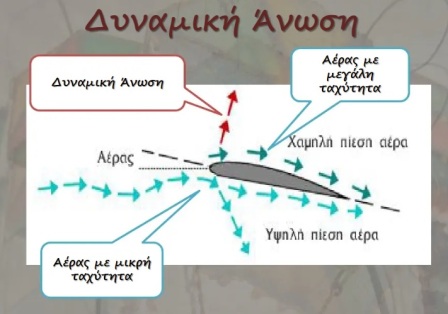
Πίσω από το πέταγμα του χαρταετού βρίσκεται και ο 3ος Νόμος του Νεύτωνα (Δράση - Αντίδραση). Πράγματι, η διευθύνουσα γραμμή (σχοινί) κρατά τον χαρταετό υπό γωνία (γωνία προσβολής), με τον άνεμο, ώστε ο αέρας να εκτρέπεται προς τα κάτω. Αυτό δημιουργεί μια αντίθετη και προς  τα πάνω δύναμη που εξισορροπεί τη δύναμη της βαρύτητας που ασκείται στον χαρταετό και ονομάζεται «Δυναμική Άνωση», αφού η εκτροπή του αέρα απαιτεί να ασκηθεί δύναμη από τον χαρταετό στον αέρα, οπότε και ο αέρας με τη σειρά του ασκεί δύναμη ίσου μέτρου και αντίθετης κατεύθυνσης στον χαρταετό!

Τα ζύγια διαφόρων τύπων διαμοιράζουν την τάση του σπάγκου από τον οποίο κρατά με τον χαρταετό, προκειμένου αυτός να αποκτήσει ευστάθεια.Τα ζύγια ρυθμίζουν τη γωνία προσβολής του χαρταετού, τη γωνία δηλαδή που σχηματίζει ο κύριος άξονας του χαρταετού με τη διεύθυνση πνοής του ανέμου. Η γωνία προσβολής του χαρταετού πρέπει να είναι μεγαλύτερη όταν πνέει ελαφρός άνεμος και μικρότερη όταν πνέει δυνατός άνεμος.

H ουρά στον χαρταετό δεν είναι μόνο διακοσμητική, αλλά εξυπηρετεί δύο βασικούς σκοπούς: α) η αντίστασή της στον αέρα σταθεροποιεί τον χαρταετό, κάνοντάς τον λιγότερο ευαίσθητο στους δυνατούς ανέμους και β) ρυθμίζει τη γωνία προσβολής του χαρταετού ανάλογα με τον άνεμο που φυσά.

Για να κατασκευάσουμε, όμως, έναν εξάγωνο χαρταετό, χρειάζεται να επιστρατεύσουμε γνώσεις από τα μαθηματικά και συγκεκριμένα από τη γεωμετρία. Πώς ορίζουμε το κανονικό εξάγωνο; ποιες είναι οι ιδιότητες του; Πώς κατασκευάζουμε ένα κανονικό εξάγωνο; Η κατασκευή ενός κανονικού εξαγώνου στη γεωμετρία προϋποθέτει την κατασκευή ενός κύκλου. Πώς, όμως, μπορούμε να χαράξουμε έναν κύκλο χωρίς διαβήτη, τόσο μεγάλο που να εγγράφεται το εξάγωνο του χαρταετού μέσα στον κύκλο; Ή μήπως η απάντηση κρύβεται στις επίκεντρες γωνίες; Τι σχέση έχει αυτό με τις γωνίες του γνώμωνα που χρησιμοποιούμε ως γεωμετρικό όργανο;

Αφού επίλυσαν τα γεωμετρικά προβλήματα οι μαθήτριες του STEM, ασχολήθηκαν με την κατασκευή του χαρταετού.

Στο τέλος, οργανώθηκε και η επιχείρηση: “πέταγμα του χαρταετού”!

Και αν νομίζετε ότι εδώ τελειώνει η επιστήμη, θα σας πούμε ότι ο Βενιαμίν Φράνκλιν με τη βοήθεια του πετάγματος του χαρταετού ανακάλυψε το αλεξικέραυνο!